In this article, we will see how to solve the famous Young Tableau problem given in Cormen using Java and C++ code. Young Tableau is a very popular problem in the world of Data Structure and Algorithms to deal with. It was first introduced by a mathematician Alfred Young in the year 1900. It provides a very convenient way to describe the group representations of the symmetric and general linear groups. Here we will try to understand this theory and know how to perform different operations using Java and C++ code examples. So without further delay, let's begin !!

 

Solved: Young Tableau Problem in Cormen using Java and C++

Also Read: Solved "java is not recognized as an internal or external command"

An M × N Young tableau is an M × N matrix such that the entries of each row are sorted from left to right and the entries of each column are sorted from top to bottom. Some of the young tableau entries may be infinity(INT_MAX in cpp and Integer.MAX_VALUE in Java), which we treat as non-existent elements. Thus young tableau can hold n <= M*N finite numbers.

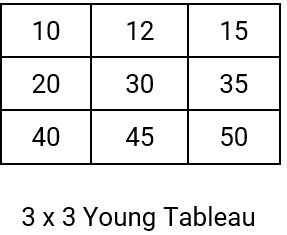
Young Tableau is similar to min heap except the condition that in min heap we only deal with 1D array and in Young Tableau we deal with 2D Array.

 

Insert Operation 

To insert new element into Young Tableau (Non Full Young Tableau), we place the new element at bottom right corner and then move that element to its correct position upwards and leftward with following procedure:-

a) If the current element (i, j) is smaller than the (i-1, j) element then we will swap both element.

b) If the current element (i, j) is smaller than the (i, j-1) element then we will swap both element.

c) In this way we will get the (i, j) greater than both (i-1, j) and (i, j-1) and the newly inserted element will be put at its correct position.

The Time complexity of inserting a new element in Young Tableau is O(M + N).

 

Extract Minimum Operation 

The minimum element of Young Tableau is present at (0,0) cell. We can easily access that and print that element in O(1) time.

 

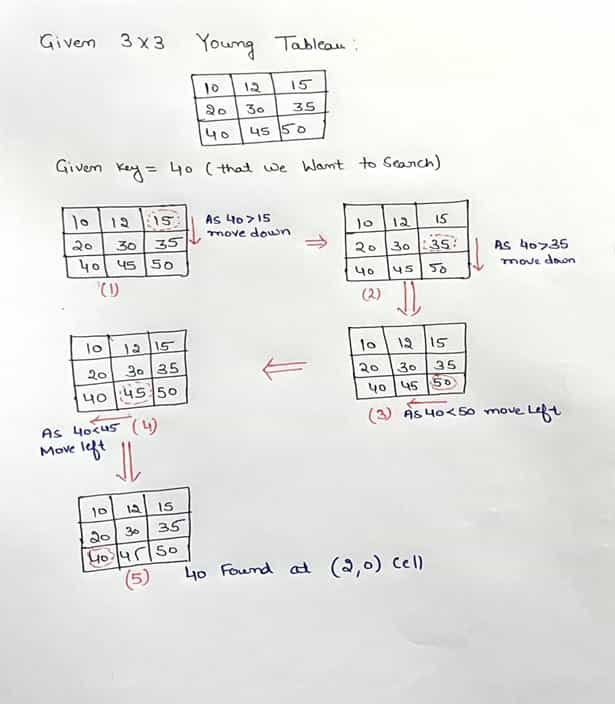
Search Operation

A naive way to search the key in the Young tableau is to go through each element and check whether given element is present or not, but the time complexity in this case will be O(M x N). We can solve this problem with better time complexity of O(M + N). We will use the fact the each row is sorted from left to right and each column is sorted from top to bottom.

a) We will start our search from top right corner of matrix (0, N-1) cell.

b) If the key is equal to current element that means key is present in the matrix.

c) If the key is smaller than the current element we will decrement the column index by one(move left).

d) If the key is greater than the current element we will increment the row number by one (move down).

We will repeat this process until the row index and column index are not out of bound.

 

Delete Operation 

To delete the given element from Young Tableau we replace that element with infinity. But due to this the sorted arrangement of given row and column get disturbed and now we will need to rearrange the matrix elements. We will move the infinity towards right and bottom with following procedure:-

a) If the current element (i, j ) is smaller than the (i-1, j) element then we will swap both element.

b) If the current element (i, j) is smaller than the (i, j-1) element then we will swap both element.

c) In this way we will get the (i, j) greater than both (i-1, j) and (i, j-1) and the newly inserted element will be put at its correct position.

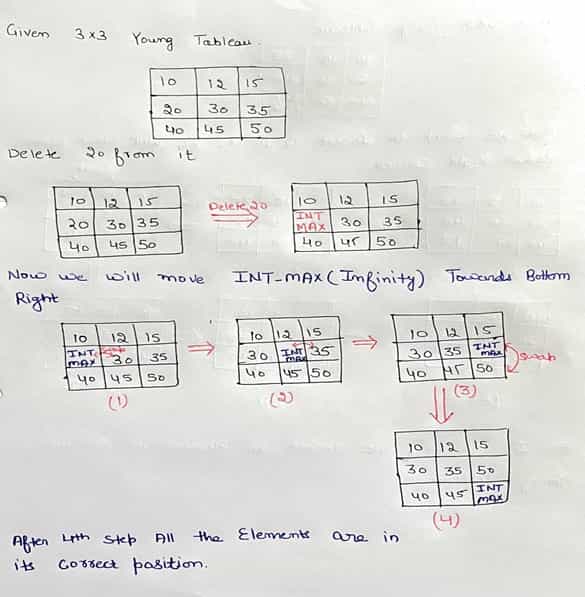
The Time complexity of Delete operation in Young Tableau is O(M + N).

 

Java Code

import java.io.*;

class GFG {
    public static void swap(int[][]tableau,int row1,int col1,int row2,int col2)
    {
       int a=tableau[row1][col1];
       tableau[row1][col1]=tableau[row2][col2];
       tableau[row2][col2]=a;
    }

    public static void util(int[][] tableau, int row, int col)
    {
       //base condition
       if (row == 0 && col == 0) {
       return;
    }

    // handle first row specially as there is no above element for this row
    if (row == 0)
    {
        if (tableau[row][col] < tableau[row][col-1])
        {
            swap(tableau,row,col,row,col-1);
            util(tableau, row, col - 1);
        }
        return;
    }

    // handle first column separately as there is no left column
    if (col == 0)
    {
        if (tableau[row][col] < tableau[row-1][col])
        {
           swap(tableau,row,col,row-1,col);
           util(tableau, row - 1, col);
        }
        return;
    }
    //go up
    if (tableau[row][col] < tableau[row-1][col])
    {
        swap(tableau,row,col,row-1,col);
        util(tableau, row - 1, col);
    }
    //go left
   if (tableau[row][col] < tableau[row][col-1])
   {
        swap(tableau,row,col,row,col-1);
        util(tableau, row, col - 1);
   }
}

   public static void insert(int[][] tableau,int key){
      int M=tableau.length;
      int N=tableau[0].length;
      if(tableau[M-1][N-1]!=Integer.MAX_VALUE){
         System.out.println("Can not insert new element as tableau is already full");
         return;
      }
      tableau[M-1][N-1]=key;
      util(tableau,M-1,N-1);
   }

   public static void search(int[][] tableau,int key){
      int i=0;
      int j=tableau[0].length-1;
      while(i<tableau.length && j>=0){
          if(tableau[i][j]==key){
             System.out.print("the given key is found at "+i+"th row and "+j+"th column \n");
             return;
          }else if(key>tableau[i][j]){
             i++;
          }else{
             j--;
          }
      }
      System.out.println("given key is not present inside young tableau");
   }

   public static void extractMin(int[][] tableau){
        System.out.print("Minimum element in young tableau is "+ tableau[0][0]+"\n");
   }

   public static void makeTableau(int[][] tableau, int row, int col){
       //M x N Young tableau
       int M=tableau.length;
       int N=tableau[0].length;

       // get the values present at the bottom and right cell of the current cell
       int bottom = (row + 1 < M) ? tableau[row + 1][col] : Integer.MAX_VALUE;
       int right = (col + 1 < N) ? tableau[row][col + 1] : Integer.MAX_VALUE;

       if (bottom == Integer.MAX_VALUE && right == Integer.MAX_VALUE) {
           return;
       }
       if(bottom < right) // go down
       {
          swap(tableau,row,col,row+1,col);
          makeTableau(tableau,row+1,col);
       }
       else // go right
       {
          swap(tableau,row,col,row,col+1);
          makeTableau(tableau,row,col+1);
       }

   }

   public static void deleteElement(int[][] tableau,int row,int col){
       //base case
       if(row >= tableau.length || col>= tableau[0].length){
           return;
       }
       //to delete the elementat (i,j) make it as infinity
       tableau[row][col]=Integer.MAX_VALUE;

      //fix the young tableau property
      makeTableau(tableau,row,col);
   }

   public static void printTableau(int[][] tableau){
       for(int i=0;i<tableau.length;i++){
           for(int j=0;j<tableau[i].length;j++){
               System.out.print(tableau[i][j] + " ");
           }
           System.out.println();
       }
   }

   public static void main(String[] args) {
   int[][] tableau = {{10,15,35},{20,30,40},{45,50,Integer.MAX_VALUE}};
       printTableau(tableau);
       insert(tableau,12);
       printTableau(tableau);
       search(tableau,40);
       extractMin(tableau);
       deleteElement(tableau,1,0);
       printTableau(tableau);
   }
}

 

C++ Code

#include <bits/stdc++.h>
using namespace std;

void util(vector<vector<int>> &tableau, int row, int col)
{
    //base condition
    if (row == 0 && col == 0) {
        return;
    }

    // handle first row specially as there is no above element for this row
    if (row == 0)
    {
        if (tableau[row][col] < tableau[row][col-1])
        {
            swap(tableau[row][col], tableau[row][col-1]);
            util(tableau, row, col - 1);
        }
        return;
    }

    // handle first column seperately as there is no left column
    if (col == 0)
    {
        if (tableau[row][col] < tableau[row-1][col]) 
        {
            swap(tableau[row][col], tableau[row-1][col]);
            util(tableau, row - 1, col);
        }
        return;
    }

    //go up
    if (tableau[row][col] < tableau[row-1][col])
    {
        swap(tableau[row][col], tableau[row-1][col]);
        util(tableau, row - 1, col);
    }
 
    //go left
    if (tableau[row][col] < tableau[row][col-1])
    {
        swap(tableau[row][col], tableau[row][col-1]);
        util(tableau, row, col - 1);
    }
}

void insert(vector<vector<int>>&tableau,int key){
    int M=tableau.size();
    int N=tableau[0].size();
    if(tableau[M-1][N-1]!=INT_MAX){
        cout<<"Can not insert new element as tableau is already full"<<endl;
        return;
    }
    tableau[M-1][N-1]=key;
    util(tableau,M-1,N-1);
}

void search(vector<vector<int>>tableau,int key){
    int i=0;
    int j=tableau[0].size()-1;
    while(i<tableau.size() && j>=0){
       if(tableau[i][j]==key){
          cout<<"the given key is found at"<<i<<"th row and"<<j<<"th column"<<endl;
           return;
       }else if(key>tableau[i][j]){
           i++;
       }else{
           j--;
       }
    }
    cout<<"given key is not present inside young tableau"<<endl;
}

void extractMin(vector<vector<int>>tableau){
   cout<<"Minimum element in young tableau is: "<<tableau[0][0]<<endl;
}

void makeTableau(vector<vector<int>> &tableau, int row, int col)
{
    // M × N Young tableau
    int M = tableau.size();
    int N = tableau[0].size();

    // get the values present at the bottom and right cell of the current cell
    int bottom = (row + 1 < M) ? tableau[row + 1][col] : INT_MAX;
    int right = (col + 1 < N) ? tableau[row][col + 1] : INT_MAX;

    if (bottom == INT_MAX && right == INT_MAX) {
        return;
    }

    if (bottom < right) // go down
    {
        swap(tableau[row][col], tableau[row + 1][col]);
        makeTableau(tableau, row + 1, col);
    }
    else // go right
    {
        swap(tableau[row][col], tableau[row][col + 1]);
        makeTableau(tableau, row, col + 1);
    }
}

void deleteElement(vector<vector<int>>&tableau, int row, int col){
   // base case
   if (row >= tableau.size() || col >= tableau[0].size()) {
       return;
   }
   // to delete the element at `(i, j)`, make it as infinity
   tableau[row][col] = INT_MAX;

   // fix the Young tableau property
   makeTableau(tableau, row, col);
}

void printTableau(vector<vector<int>> tableau){
    for(int i=0;i<tableau.size();i++){
       for(int j=0;j<tableau[0].size();j++){
          cout<< tableau[i][j]<<" ";
       }
       cout<<endl;
    }
}

int main() {
      vector<vector<int>>tableau={{10,15,35},{20,30,40},{45,50,INT_MAX}};
      printTableau(tableau);
      insert(tableau,12);
      printTableau(tableau);
      search(tableau,40);
      extractMin(tableau);
      deleteElement(tableau,1,0);
      printTableau(tableau);
}

 

Conclusion

In this article we have gone through what is young tableau and the different operations in young tableau like insert operation, search operation, extract minimum operation and delete operation. We also saw time complexity of each operation and at last we implemented all the above features in java and C++.